Daniel Sánchez Sánchez
daniel.sanchezs@udea.edu.co
Instituto de Filosofía
Universidad de Antioquia

En este ensayo se propone mostrar desde la teoría de control tres criterios o procesos que pueden considerarse constitutivos de todo aprendizaje: la autocorrección, el procesamiento de los errores pasados y presentes, y la predicción. Para esto, se explicará cómo estos criterios surgen de los tipos de controladores, según sus módulos y complejidad. Por último, se expondrá el funcionamiento de las redes neuronales y de los sistemas expertos, en términos de estos mismos criterios.

Comencemos por sistemas simples. En teoría de control, uno de los sistemas más básicos es el control On-Off, también denominado en español todo-nada o encendido-apagado. Este tipo de sistema puede ser tan simple que, en algunos casos, ni siquiera requiere de circuitos, ni sistemas mecánicos… En general, el control On-Off es un sistema de lazo cerrado, o sea un sistema que se autocorrige. Veamos dos ejemplos: un horno está pensado para modificar la temperatura en un espacio cerrado; un control ON-OFF para un horno sería uno tal que contenga un sensor de temperatura y un switch de encendido y apagado: si la temperatura está por encima entonces se apaga el resistor y si está por debajo se enciende. Eventualmente, el sistema llegará a la temperatura deseada. Pongamos otro ejemplo, ahora uno en el que no se requiera nada electrónico ni mecánico: si yo quiero que un tanque en el que cae agua no se llene del todo, sino sólo hasta cierto límite, entonces puedo hacer un control On-Off simplemente abriendo un hueco justo por encima del límite que no quiero que pase. Así, si el nivel del agua está por debajo, el tanque se llenará, si está por encima, se derramará el agua por el agujero. Dicho esto, hagamos la pregunta: ¿este sistema aprende o no? Lo que ya extraemos del caso es que el sistema On-Off al menos cumple un criterio importante: la autocorrección, gracias a que es un sistema de lazo cerrado.

Subamos ahora de complejidad. Supongamos que requerimos controlar algo con más cuidado, por lo que decidimos usar lo que se denomina un control proporcional (o control P). Este tipo de control se distingue del anterior en que tiene en cuenta cuánto le falta a la variable para llegar al valor deseado, o sea cuánto error. En el ejemplo del horno, un control On-Off sólo se encuentra entre dos estados de cambio: máximo o nulo. En cambio, el control P modifica gradualmente el cambio (la potencia, el calentamiento, el flujo…); de forma que, en nuestro ejemplo, P usa la potencia máxima al principio (cuando el espacio está más frío) y ésta se va disminuyendo a medida que llegamos a la temperatura deseada. El defecto de los controles P es que, o bien pueden desestabilizar el sistema o bien no llegar ni siquiera al valor deseado. De nuevo, preguntemos: un sistema como el control P, ¿aprende? Lo importante es que aquí la autocorrección es controlada gradualmente: el sistema distingue un error mayor de uno menor.

Aumentemos aún más la complejidad del control añadiendo otras dos funciones. Un control PID (es decir: proporcional, integral y derivativo) ya no sólo controla gradualmente una variable, sino que también tiene en cuenta, por su módulo de función integrativa (I), el período de los estados pasados hasta el presente (suma progresivamente los errores); y por su módulo derivativo, tiene en cuenta la tendencia o pendiente (vectores en la fig. 1) del cambio del error (o sea, predice los estados inmediatamente próximos) para amortiguarla. Pongamos ejemplos, cuando uno quiere hacer sapitos en el agua lanzando piedras debe aprender de los errores pasados (función integrativa) para perfeccionar la técnica, pero es imposible predecir cómo saldrá el siguiente lanzamiento (no hay función derivativa). En cambio, en los juegos competitivos se requiere intentar constantemente predecir el comportamiento de los otros jugadores, además de tener en cuenta experiencias pasadas (o sea, requiere las capacidades del PID). En fin, nuevamente planteo la pregunta: un control PID, ¿es un sistema que aprende? Ya con esto tenemos los dos criterios restantes: memoria y capacidad predictiva.

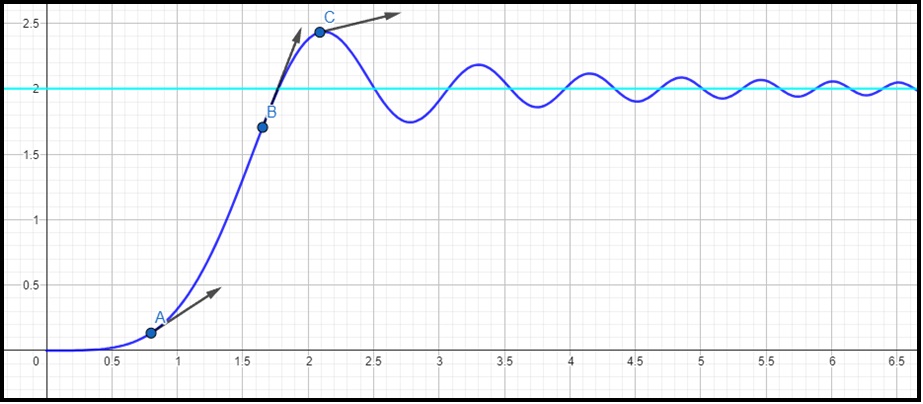
Figura 1. Puntos A, B y C y sus tendencias locales.

Como vimos, la teoría de control nos ha dado un marco de análisis para el procesamiento del error en un proceso de aprendizaje. Más precisamente, si partimos de las características del control PID como base de todo aprendizaje, la teoría nos dice que el aprendizaje tiene un objetivo (el valor deseado), que para llegar a él hay que tener en cuenta el error actual (P), los errores previos (I), y los próximos pasos a seguir como error futuro (D). Y, además, que la base de todo ello es la autocorrección (lazo cerrado). Pero esta teoría no nos habla de los sistemas en sí, ni de su estructura. Por ejemplo, respecto al tanque de agua, yo podría en su lugar haber implementado un sistema con un sensor y una válvula gradual que modificara el caudal de entrada; o bien podría pagarle a una persona para que vigilara el nivel y él mismo detuviera el proceso de llenado, etcétera. Lo que sí podemos hacer con la teoría de control es analizar las capacidades de aprendizaje de los sistemas. Esto haremos ahora con los sistemas de inteligencia artificial.

Analicemos primero el proceso de aprendizaje de un perceptrón. Un perceptrón simple, sin retropropagación, por sí solo puede entenderse como un control proporcional de lazo abierto, o sea que no se autocorrige. La corrección depende de un agente externo que modifique los pesos. Ya con la retropropagación el perceptrón se puede considerar un sistema de lazo cerrado, pero sólo si se hace el reparo de que la diferencia con los ejemplos que vimos es que ni el progreso ni el error son funciones continuas. En otras palabras, en el perceptrón no hay un estado posterior cuyo error esté relacionado con el del estado anterior, sino que el error se corrige absolutamente para cada caso. Por cada activación del perceptrón se diría que hay un control netamente proporcional, porque los pesos son una constante proporcional como lo es el módulo P; de hecho, un perceptrón es, en cada activación, un control multiproporcional, según la cantidad de capas y de neuronas.

Para hablar de una función integrativa (I) tendríamos que abstraernos del funcionamiento del perceptrón en cada activación particular; así, a medida que la retropropagación modifica los pesos, podríamos decir que integra los errores pasados en cada uno de ellos, como una función que los hace converger a un valor idóneo. Aunque, la acotación por hacer es que la función integral no se cumple en el perceptrón como un módulo del sistema; o sea, no es una operación matemática interna, sino que está como una propiedad emergente, producto de la retropropagación. Por lo tanto, la función integrativa se cumple de otra manera distinta. Por otra parte, la función derivativa (o predictiva) habría que pensarla también abstractamente. La función predictiva se vería en el hecho de que la retropropagación, cuando corrige los pesos según el caso actual, prepara el perceptrón para casos semejantes en el futuro. De hecho, dado que para el perceptrón no hay continuidad en el error, no hay función derivable y por tanto hablar de «función derivativa» no tiene sentido. En el perceptrón la predicción es estadística. No obstante, desde la teoría de control, un perceptrón es funcionalmente equivalente a un control PID.

Analicemos ahora los sistemas expertos. Un sistema experto puede contar con algoritmos internos que representen sistemas de control PID (puesto que son esencialmente modelos matemáticos para el tratamiento de información), aunque el sistema total no necesariamente es un PID, sólo lo usa. Esencialmente, el sistema experto es un control de lazo abierto; es decir, no se corrige por sí mismo. La corrección depende de alguien que optimice el algoritmo. Además, el sistema experto tampoco se hace para modificar un valor constantemente, sino que toma un solo valor de entrada para entregar uno de salida. En pocas palabras, el sistema experto no cumple ni siquiera el criterio de autocorrección. Si comparamos, el aprendizaje en una red neuronal sin retropropagación sería funcionalmente equivalente al de un sistema experto: ambos dependen exclusivamente de la constante optimización humana.

Conclusiones: (1) la teoría de control nos ofrece tres criterios de aprendizaje, criterios útiles para comprender cómo funcionan las máquinas y discernir entre ellas; (2) si aceptamos los tres criterios como suficientes para caracterizar el aprendizaje, entonces diríamos que las redes neuronales y los sistemas con controles PID efectivamente «aprenden», y que algunos otros sistemas como los expertos o los perceptrones sin retropropagación no lo hacen. No obstante, no creo que los tres criterios expliquen la extensión del aprendizaje humano, ni tampoco las parenéticas posibilidades de optimización de las redes neuronales. Tenemos, por ejemplo, una capacidad de respuesta frente a múltiples contextos, sean simultáneos o aleatorios, que escapa al alcance analítico de la teoría de control. Lo mismo se diría del carácter evidentemente intencional en el aprendizaje humano. Lo que esto enseña es, una vez más, la suntuosa complejidad de las capacidades humanas.

Referencias

Ogata, K. (2010). Ingeniería de control moderna (5a. ed). Pearson Educación.

Sontag, E. D. (1998). Mathematical control theory: Deterministic finite dimensional systems (2nd ed). Springer.